
每周完成一个 ARTS:
Algorithm: 每周至少做一个 LeetCode 的算法题
Review: 阅读并点评至少一篇英文技术文章
Tips: 学习至少一个技术技巧
Share: 分享一篇有观点和思考的技术文章
122. Best Time to Buy and Sell Stock II
题目:122. Best Time to Buy and Sell Stock II
难度:Easy
题意:给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。 设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
示例 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
示例 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
解法:
本题的解法其实也非常直接,从数学上来讲,因为我可以无限次买进卖出,只要每次卖出的价格比买进的价格高,那么就是稳赚不赔并且能够获取最多利润的。那么我们只要遍历价格数组,只要当前价格比前一个价格高,那么就卖出,如此重复并且将利润累加,我们就能获得最大的利润。
代码:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
max_profit = 0
for i in range(1, len(prices)):
if prices[i] > prices[i-1]:
max_profit += prices[i] - prices[i-1]
return max_profit
时间复杂度 O(n),空间复杂度 O(1)。
Time Series in Python — Exponential Smoothing and ARIMA processes
本周阅读的是 Medium 上的一篇讲述使用 Python 对时间序列进行分析的一篇文章,《Time Series in Python — Exponential Smoothing and ARIMA processes》。本文讲述了如何使用 Python 对时间序列进行指数平滑和 ARIMA 过程的建模。
文章首先举例讲述了时间序列的几种存在情况,然后说明了时间序列的四大属性:trend(趋势)、seasonality(季节性)、cyclicity(周期性)、residual(残差)以及时间序列的分解,之后使用简单的例子对平稳性及其检验和自相关与偏自相关函数进行了说明,最后分别对几种指数平滑的模型和 ARIMA 模型的建模过程进行了详细的讲解。
本文是从 Python 的角度对时间序列建模展开讲解,并且给出了较为详细的代码,使用的是 statsmodels 库。这个库中没有和 R 中 autoarima() 对标的函数,所以如果想要实现自动调参的功能,可以利用 aic/bic 准则,grid search 出最佳的参数。
Vim 中的两个补全操作
Vim 中有两个常用的不依赖插件的补全操作:
另外有一个输出当前路径的命令:
:r! echo % # 输出当前文件名
:r! echo %:p # 输出完整路径名
决策树(一):决策树学习的基本概念
本文是我阅读李航老师《统计学习方法》中决策树章节的部分笔记,分享给大家。
决策树是一种基本的分类与回归方法。我们这一篇文章对决策树模型的定义、其与 if-then 规则和条件概率的关系、以及决策树学习的基本方法进行了归纳总结。

一棵简单的决策树如上图所示,是一种树形结构,由结点和有向边组成。图中,圆形表示内部结点,内部结点表示一个特征或者属性,方形表示叶子结点,叶子结点表示分类结果,即一个类。
决策树可以看成一个 if-then 规则的集合:对决策树的根节点到叶子结点的每条路径都构建一条规则,路径上的内部结点表示的特征对应于规则的条件,叶子结点则对应着规则的结论。这样,这个 if-then 规则有一个重要的性质,即互斥且完备。
决策树还可以看成给定特征条件下的条件概率分布。这种条件概率分布可以理解为对特征空间的一个划分(partition)。如下图所示:
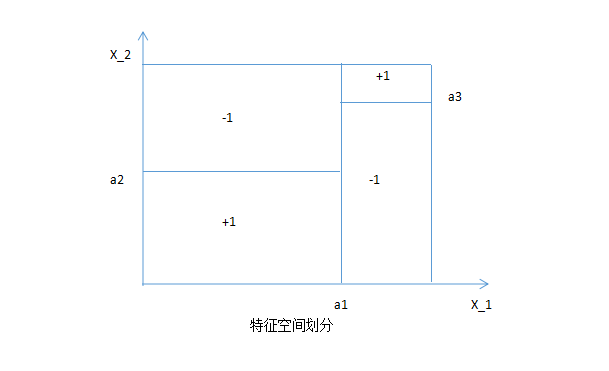
在这种划分下,特征空间被划分为几个互不相交的 cell 或 region,每个 cell 都定义了一个类。这种概率分布即构成了一个条件概率分布。
决策树学习的目的就是:根据给定的训练数据构建一个决策树模型,使它能够对实例进行争取的分类。本质上,决策树学习是从训练集中归纳出一组分类规则的过程,那么符合训练集的决策树可能有很多个(也可能一个都没有),决策树学习需要从众多树中选择一棵不仅对训练集有较好拟合的树,并且要求这棵树对未知数据也有较好的泛化能力。那么这个过程就是一个 NP 完全问题(关于什么是 NP 问题与决策树的 NP 完全问题,请参考这篇文章),意味着我们无法使用计算机在多项式时间复杂度内找出全局最优解,也就从另一个角度说明,决策树最后的结果,是在每一步、每一个节点上做的局部最优选择。
决策树学习的过程如下(引自《统计学习方法》):
开始,构建根节点,将所有的训练数据集都放在根节点,选择一个最优特征,按照这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下获得最好的分类。如果这些子集已经能够被基本正确分类,那么构建叶节点,并将这些子集分到对应的叶节点中去;如果还有子集不能够被基本正确分类,那么就对这些子集新的选择最优特征,继续对其进行分割,构建相应的结点。如此递归下去,直到所有的训练数据子集被基本正确分类,或者没有合适的特征为止。最后每个子集都被分到叶节点上,即都有了明确的分类,这就生成了一棵决策树。 以上方法生成的决策树可能对训练数据有很好的分类能力,但是对未知数据集未必有很好的分类能力,即可能发生过拟合的现象。我们需要对已生成的树自下而上进行剪枝,将树变得更简单,从而使它拥有更好的泛化能力。
可以看出,决策树学习算法大致包含三个步骤:特征选择、决策树生成与决策树的剪枝。
下一篇文章我们更新决策树学习中的特征选择与信息增益相关的内容。