ARTS 第 7 周

每周完成一个 ARTS：
Algorithm: 每周至少做一个 LeetCode 的算法题
Review: 阅读并点评至少一篇英文技术文章
Tips: 学习至少一个技术技巧
Share: 分享一篇有观点和思考的技术文章

Contents:

Algorithm

杨辉三角 II 题目：119. Pascal’s Triangle II

难度：Easy

题意：给定一个不大于 33 的非负数 k，返回杨辉三角的第 k 行。

示例：

Input: 3
Output: [1,3,3,1]

要求：优化算法到到 O(k) 空间复杂度

解法：

这道题目和上周的杨辉三角 I 很相像，只要找到数学公式即可轻易做出。

杨辉三角有一个性质是，它的第 n 行的第 i 个数字（n 和 i 均从 0 开始）为：$C_n^i = \frac{n!}{(n-i)! \times i!}$。那么由第 i 个数字就可以很容易推出第 i+1 个数字：$C_n^{i+1} = \frac{n!}{(n-i-1)! \times (i+1)!} = \frac{n-i}{i+1} \times C_n^i$。

那么代码也就很容易写了:

class Solution(object):
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        if rowIndex > 33 or rowIndex < 0:
            return []

        ans = [1] * (rowIndex + 1)
        for i in range(rowIndex):
            ans[i+1] = ans[i] * (rowIndex - i) // (i + 1)

        return ans

时间和空间复杂度均为 O(n)。

Review

Deep inside: Autoencoders

这篇文章选自 Medium 上 Towards Data Science 专栏。对自编码器有了一个大致的介绍。

本文先介绍了自编码器的基本结构：自编码器由两部分组成，编码器和解码器。

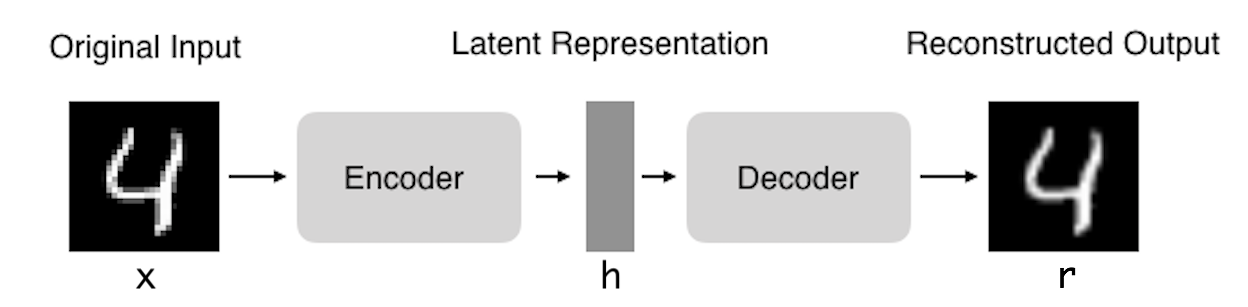
整个自编码器可以用函数 g(f(x)) = r 来表示，我们希望输出 r 与输入 x 尽量接近。这样做的目的在于，潜在表征 h 是非常有价值的。

自动编码器是从数据示例中自动学习的（无监督学习），这意味着可以很容易地将这个算法应用到某个数据集中，来取得良好的性能，且只需要适当地训练数据而不需要任何新的特征工程。

需要注意的是，自编码器在图像压缩任务上表现不好，因为他只是在某个给定的数据集上训练，所以也只能在相似的图像上取得不错的效果，而对于一般的图像，JPEG 等图像压缩算法通常有更好的效果。

之后作者也对几种不同的自编码器进行了讨论，如 Vanilla 自编码器、多层自编码器、卷积自编码器和正则化自编码器。有兴趣的同学可以去看看。

Tips

在终端中使用代码编辑器打开文件或者目录 只要在你的 .zshrc 中添加这几行，之后 source 一下即可：

alias atom='/Applications/Atom.app/Contents/MacOS/Atom'
alias subl='/Applications/Sublime\ Text.app/Contents/SharedSupport/bin/subl'
alias code='/Applications/Visual\ Studio\ Code.app/Contents/Resources/app/bin/code'

Share

播客分享

我本人比较喜欢听播客节目，这周分享自己常用的几个 iOS 播客客户端和常听的几个播客节目。

客户端：

节目：